Definition of probability says the probability of certain event is ratio of number of desired outcomes of an experience to the number of possible outcomes of that experiment (if they are equiprobable).
Number of letters in the alphabet = 26
for the letter VALVE
There is one V, A, L, E in the set of aplhabet
So

For the propbability of letter VALVE
![\text{ Probability of VALVE = Probability of V+}Probability\text{ of A+ Probability of L+}Probability\text{ of V+ Probability of E}]()
So, substitute the value:
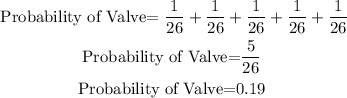
Answer : 0.19