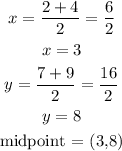Answer:
The distance between the points is:
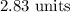
The midpoint is at;
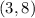
Step-by-step explanation:
Given the set of ordered pairs;
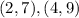
Firstly, let us find the distance between the two points.
The formula for calculating the distance between two points is;
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
substituting the given coordinates;
![\begin{gathered} (x_1,y_1)=(2,7) \\ (x_2,y_2)=(4,9) \\ d=\sqrt[]{(4-2)^2+(9-7)^2} \\ d=\sqrt[]{2^2+2^2} \\ d=\sqrt[]{8} \\ d=2.83 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/s69kmkgqw1hngo1rvbpvbp8x1jf7soq86m.png)
Secondly, let us find the midpoint;
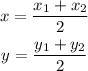
substituting the coordinates;