Question

Brad=Unproctored Placement AssessmentDue Wednesday 9:40 PM 1 Question 18A chemical company makes two brands of antifreeze. The first brand is 70% pure antifreeze, and the second brand is 95% pure antifreeze. In order to obtain110 gallons of a mixture that contains 75% pure antifreeze, how many gallons of each brand of antifreeze must be used?First brand:gallonsSecond brand:gallons

Answer 1

Let 'x' gallons of first brand and 'y' gallons of second brand antifreeze is used.

Given that the first brand is 70% pure antifreeze. It means that each gallon of this brand contains 0.70 gallons of the solute. So the amount of solute in x gallons will be,

`\begin{gathered} =0.70* x \\ =0.70x \end{gathered}`

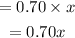
Also, it is given that the second brand is 95% pure antifreeze. So the amount of solute in 'y' gallons will be,

`\begin{gathered} =0.95* y \\ =0.95y \end{gathered}`

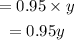
The total mixture is 110 gallons, so we can write,

`\begin{gathered} \text{Total Amount of Mixture}=\text{ Amount of first brand}+\text{Amount of second brand} \\ 110=x+y \\ x+y=110\ldots\ldots(1) \end{gathered}`

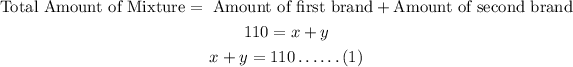
Also the mixture is 75% antifreeze. It means that each gallon of this mixture will contain 0.75 gallon solute. So the amount of solute in 110 gallons will be,

`\begin{gathered} =0.75*110 \\ =82.5 \end{gathered}`

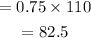
The total quantity of solute in this mixture should be equal to the sum of quantity of solutes in first and second brand,

`0.70x+0.95y=82.5\ldots\ldots(2)`

Substitute the value of 'y' from equation (1) in equation (2),

`\begin{gathered} 0.70x+0.95(110-x)=82.5 \\ 0.70x+104.5-0.95x=82.5 \\ 104.5-82.5=0.95x-0.70x \\ 0.25x=22 \\ x=88 \end{gathered}`

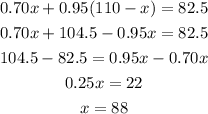
Substitute this value in equation (1) to obtain 'y' as,

`\begin{gathered} y=110-x \\ y=110-88 \\ x=22 \end{gathered}`

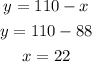
The values of 'x' and 'y' are 22 and 88 respectively.

So, the 22 gallons of first brand and 88 gallons of second brand must be used to obtain the required mixture.