Question

Sum of the arithmetic sequence- Find each sum: 5+ 9 +13 + ... +49

Answer 1

324

Step-by-step explanation

We want to find the sum of the arithmetic progression:

`5+9+13\ldots_{}+49`

To do that we apply the formula for the sum of an arithmetic sequence:

`S_n=(n)/(2)(a+l)`

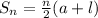
where a = first term

l = last term

n = number of terms

We have to find n by using the last term:

`a_n=a+(n-1)d`

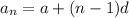
d = common difference

The common difference is 4. Therefore, we have to find n:

`\begin{gathered} 49=5+(n-1)\cdot4 \\ 49=5+4n-4 \\ 49=1+4n \\ \Rightarrow4n=49-1=48 \\ n=(48)/(4) \\ n=12 \end{gathered}`

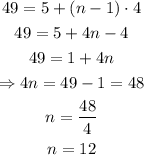
There are 12 terms.

Therefore:

`\begin{gathered} S_n=(12)/(2)(5+49)=6\cdot(54) \\ S_n=324 \end{gathered}`

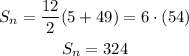
That is the sum of all the terms.