Question

Hi, can you help me answer this question, please, thank you:)

Answer 1

The lengths of the professor's classes are uniformly distributed.

A uniform distribution is also called a rectangular distribution, which is characterized by having a constant probability and is defined by two parameters, a (minimum value) and b (maximum value).

With probability density function defined as:

`f(x)=\begin{cases}(1)/(b-a);x\in\lbrack a,b\rbrack \\ 0;otherwise\end{cases}`

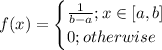
And its cumulative distribution function is defined as:

`F(x)=\begin{cases}0;xb\end{cases}`

For the defined uniform distribution, the parameters are:

a= 50.0min

b= 52.0 min

To calculate the asked probability P(X>50.8) you have to work using the cumulative distribution function, which can be defined for this particular distribution as follows:

`F(x)=\begin{cases}0;x<50.0 \\ (x-50.0)/(52.0-50.0) \\ 1;x>52.0\end{cases}`

The cumulative distribution accumulates probabilities from zero to xi, i.e. it indicates the probabilities less than or equal to a value "xi", so you'll have to rewrite the probability and work with its complement:

`P(X>50.8)=1-P(X\leq50.8)=1-F\mleft(50.8\mright)`

Since 50.8 is between the minimum and maximum values, you can calculate F(50.8) as follows:

`\begin{gathered} F(x)=(x-50.0)/((52.0-50.0)) \\ x=50.8 \\ F(50.8)=(50.8-50.0)/(52.0-50.0) \\ F(50.8)=(0.8)/(2) \\ F(50.8)=0.4 \end{gathered}`

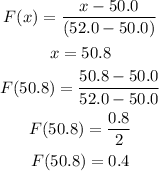
Now that we have determined the accumulated probability until 50.8 min, you can calculate its complement, i.e. the probability above 50.8min

`\begin{gathered} P(X>50.8)=1-0.4 \\ P(X>50.8)=0.6 \end{gathered}`

The probability that the class length is more than 50.8min is 0.60