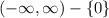Question

How can if fine the rang for f(x) and the rang for the inverse f(x)

Answer 1

The given function is

`f(x)=(4)/(x^3-1)`

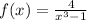
The inverse function is

`f^(-1)(x)=\sqrt[3]{(4)/(x)+1}`

Recall that the range of the function is the completely possible set of resulting values of the function.

Consider the function

`f(x)=(4)/(x^3-1)`

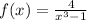
This is given function rational polynomial function so the range is negative infinity to positive infinity except for the value of x where the denominator is zero.

`x^3-1=0`
`x^3=1`
`x=1`

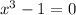
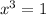
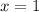
Hence the given function is not valid at x=1.

The range of the function is

`(-\infty,\infty)-\mleft\lbrace1\mright\rbrace`

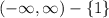
Consider the inverse function

`f^(-1)(x)=\sqrt[3]{(4)/(x)+1}`

This is inverse function rational polynomial function so the range is negative infinity to positive infinity except for the value of x where the denominator is zero.

`\sqrt[3]{x}=0`
`x=0`

Hence the inverse function is not valid at x=0.

The range of the inverse function is

`(-\infty,\infty)-\mleft\lbrace0\mright\rbrace`