Since PQ and BC are parallel, we have the following:
That is to say, triangles APQ and ABC are similar. Since they are similar, their sides are proportinal. We can then see this relation in the following equation:
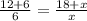
Where x is the lenght of AQ. We know rearrange the equation
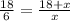
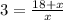
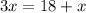
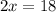
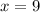
And so, the lenght of AQ is 9