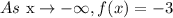Question

Complete the end behavior statement for the function shown above. As x→−∞, f(x)→

Answer 1

Given:

`f(x)=(-9x^7)/(3x^7)`

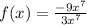
Required:

`We\text{ need to find the end behavior of f\lparen x\rparen as x}\rightarrow-\infty.`

Step-by-step explanation:

We know that the end behavior of a function is the behavior of the graph of f(x) as x approaches negative infinity.

Consider the given function.

`f(x)=(-9x^7)/(3x^7)`

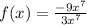
Take limit on both sides.

`\lim_(x\to-\infty)f(x)=\lim_(x\to-\infty)((-9x^7)/(3x^7))`

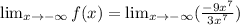
Cancel out the common multiple.

`\lim_(x\to-\infty)f(x)=\lim_(x\to-\infty)((-9)/(3))`

`\lim_(x\to-\infty)f(x)=(-9)/(3)`

`\lim_(x\to-\infty)f(x)=-3`

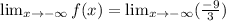
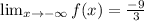
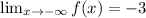
The end behavior of f(x) is -3as x approaches negative infinity

Final answer:

`As\text{ x}\rightarrow-\infty,f(x)=-3`