Question

) DeShawn invests $3,044 in a retirement account with a fixed annual interest rate of 3.14% compounded 3 times per year. How long will it take for the account balance to reach $5,341.12?

Answer 1

Consider the formula,

`A=P(1+(r)/(100))^n`

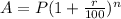
Here, P is the principal, r is the rate of interest, n is the number of periods, and A is the amount.

According to the problem, the compund interest is to be applied quarterly i.e 3 times per year, so the rate of interest is calculated as,

`r=(R)/(3)=(3.14)/(3)=(157)/(150)`

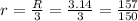
Substitute the values and solve for 'n',

`\begin{gathered} 5341.12=3044(1+(157)/(150*100))^n \\ (1.0105)^n=1.755 \end{gathered}`

Consider the formula,

`\ln (e^x)=e^(\ln x)=x`

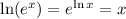
Then the equation becomes,

`\begin{gathered} \ln (1.0105)^n=\ln (1.755) \\ n\ln (1.0105)=\ln (1.755) \\ n=(\ln (1.755))/(\ln (1.0105)) \\ n=53.85 \\ n\approx54 \end{gathered}`

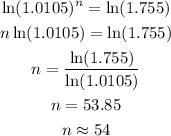
Thus, the required number of periods in 54.

The corresponding number of years will be 54 by 3 i.e. 18, since the compounding is done 3 time