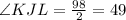Fisrt we can find the similar angles and sides so we know that:
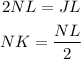
so we can replace like:
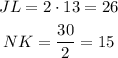
now we can find the distance KL with pithagoras so:
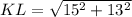
and we operate so:
![\begin{gathered} KL=\sqrt[]{225+169} \\ KL=\sqrt[]{394} \\ KL=19.8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qqcibadmyp3anxcanp6hrfc76nx73mbr32.png)
Now the angle JKM will be equal to the angle MKZ so
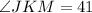
Now the angle JML will be:
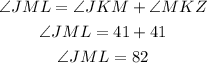
the angle MLK will be the complement of 82 on a triangle so:
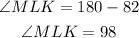
For MNL we know that the segmente MK is perpendicular to JL so the angle is:
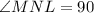
and KJL will be halve of the angle MLK so: