Question

The figure below is a kite. If m

Answer 1

Step 1:

Properties of a kite

1. Kite has 2 diagonals that intersect each other at right angles.

2. A kite is symmetrical about its main diagonal.

3. Angles opposite to the main diagonal are equal.

4. The kite can be viewed as a pair of congruent triangles with a common base.

5. Opposite angles are equal.

Step 2:

Use the property below to solve for x.

Opposite angles are equal.

Step 3

`\begin{gathered} m\angle\text{ A = 4x + 7} \\ m\angle B\text{ = 8x + 3} \\ m\angle A\text{ = m}\angle B \end{gathered}`

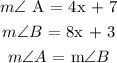
Step 4:

`\begin{gathered} 8x\text{ + 3 = 4x + 7} \\ 8x\text{ - 4x = 7 - 3} \\ 4x\text{ = 4} \\ \text{ x = }(4)/(4) \\ \text{x = 1} \end{gathered}`

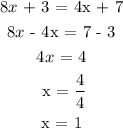
Final solution

x = 1