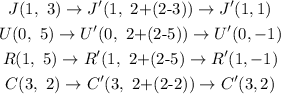Question

Find the coordinates of the verticesof each figure after the given transformation

Answer 1

Given,

The coordinates of the given figure are J(1, 3), U(0, 5), R(1, 5), C(3, 2)

Here, the reflection about only y axis,

The coordinates of the x-axis remain the same,

This finds the distance from the point to y = 2 by subtracting the point's y-coordinate from 2, then moves the point that far to the other side of y = 2 by adding 2.

The reflected coordinates are,

`\begin{gathered} J(1,\text{ 3)}\rightarrow J^(\prime)(1,\text{ 2+(2-3))}\rightarrow J^(\prime)(1,1)_{} \\ U(0,\text{ 5)}\rightarrow U^(\prime)(0,\text{ 2+(2-5))}\rightarrow U^(\prime)(0,-1) \\ R(1,\text{ 5)}\rightarrow R^(\prime)(1,\text{ 2+(2-5)}\rightarrow R^(\prime)(1,-1) \\ C(3,\text{ 2)}\rightarrow C^(\prime)(3,\text{ 2+(2-2))}\rightarrow C^(\prime)(3,2) \end{gathered}`