Question

Hello, I need some assistance with this homework question please for precalculusHW Q31

Answer 1

The given function g(x) = 4x² + 11x +6 is already in its general form in which the value of a = 4, b = 11, and c = 6. We will needing these values in the quadratic formula.

The formula is:

`x=(-b\pm√(b^2-4ac))/(2a)`

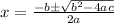
Let's plug into the formula above the values of a, b, and c.

`x=(-11\pm√(11^2-4(4)(6)))/(2(4))`

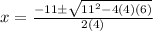
Then, solve.

a. Simplify the numbers inside the parenthesis.

`x=(-11\pm√(121-96))/(2(4))\Rightarrow x=(-11\pm√(25))/(2(4))`

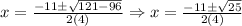
b. Get the square root of 25 and simplify the denominator.

`x=(-11\pm5)/(8)`

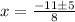
c. Separate the plus and minus symbol and solve.

`\begin{gathered} x=(-11+5)/(8)\Rightarrow x=(-6)/(8)\Rightarrow x=-(3)/(4) \\ x=(-11-5)/(8)\Rightarrow x=(-16)/(8)\Rightarrow x=-2 \end{gathered}`

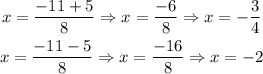
The zeros and x-intercepts are the same. They are -3/4 and -2.