PART A
We are given the following values f(x)= -3x -6 and g(x) = √-x+4
The function (fog)(x) would be gotten by inserting g(x) for the value of x in f(x)
![\begin{gathered} (\text{fog)(x)}=f(g(x)) \\ =-3(\sqrt[]{-x+4})-6 \\ =-3(\sqrt[]{4-x})-6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yvsb1qkovk8etspd45xb7r20aie7cnbclb.png)
![\text{fog(x)}=3(\sqrt[]{4-x})-6](https://img.qammunity.org/2023/formulas/mathematics/college/xnwxkrrwjng0p82lhuiwf7eab7c5wxqgny.png)
We can find the domain of (f°g)(x) by first finding the domain of g(x)
The domain of g(x) is the values of x for which g(x) is defined.
g(x) is defined for the values of x below
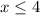
We then also need to find the domain of fog
fog(x) will not exist for the values of x below:
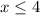
Since this coincides with the domain of g(x), therefore the domain of fog(x) is
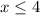
PART B
The function (gof)(x) would be gotten by inserting f(x) for the value of x in g(x)
![\begin{gathered} \text{gof(x)}=g(f(x) \\ =\sqrt[]{4-(-3x-6)} \\ =\sqrt[]{3x+10} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8g3109aov7e0bjpcr09nxvc6pjaiwe8ais.png)
Therefore, the value of gof(x)
![gof(x)=\sqrt[]{3x+10}](https://img.qammunity.org/2023/formulas/mathematics/college/12no0ojoqoe9oq69p27oilmeit4zvlh06c.png)
We can find the domain of (g°f)(x) by first finding the domain of f(x)
The domain of f(x) is the values of x for which f(x) is defined.
f(x) is defined for the values of x below
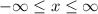
The above indicates f(x) is defined for all real numbers
We then also need to find the domain of gof
gof(x) will not exist for the values of x below:
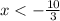
Excluding the above from the domain of f(x)
We would therefore have the domain of gof(x) as
