Question 1 : Janae can find out when she first hit the water by finding out the distance of travel, as well as her speed of travel
Question 2 :
Given that her height above the water can be modeled using the function below:
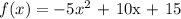
We can obtain her vertical distance of travel from the diving board to the point where she starts to descend
At the turning point,
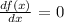

Hence, Jane travelled a distance of 10 units upwards and (10 + 15)unit downwards
At the turning point, her velocity is zero, using the relation below we can find her initial velocity and then the time it took
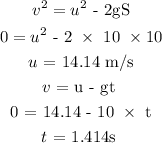
From the turning point, her velocity changes from 0