Question

Please help!! Find the number if intercepts of the graph of the function f(x)=x^2-2x+5

Answer 1

Factoring a polynomial

We know that a function intercepts x-axis when y = 0.

For the following function:

`\begin{gathered} f(x)=x^2-2x+5 \\ y=x^2-2x+5 \end{gathered}`

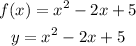
we want to know which values should have x so y = 0, then

`\begin{gathered} y=x^2-2x+5 \\ 0=x^2-2x+5 \end{gathered}`

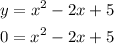
We rearrange the function so it can be expressed in the perfect square polynomial form:

x² - 2x + 5 = 0

x² + 2(- 1x) = -5

x² + 2(- 1x) + 1 = -5 + 1

x² + 2(- 1x) + 1 = - 4

(x - 1) ² = -4

We know must clear x from the equation:

(x - 1) ² = -4

x - 1 = √ (-4)

x - 1 = √ (-4) + 1

Since

√ (-4) doesn't exist because -4 is a negative number, then, this function has no intercepts with x-axis

Answer: A