Question

Tom will rent a car for the weekend. He can choose one of two plans. The first plan has an initial fee of 59.96 and costs an additional $0.15 per mile driven. The second plan has an initial fee of $53.96 and costs an additional $0.20 per mile driven. How many miles would Tom need to drive for the two plans to cost the same?

Answer 1

First, let's define expressions for the different rental plans. Let x be the miles driven for both of the plans.

We would have the following:

Plan A: $59.96 initial fee, $0.15 per mile driven

`A=59.96+0.15x`

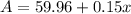
Plan B: $53.96 initial fee, $0.20 per mile driven

`B=53.96+0.20x`

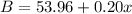
Now, since we want to know the required miles driven for the plans to cost the same, we'll have the relation

`A=B`

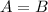
This way, we would have the equation

`59.96+0.15x=53.96+0.20x`

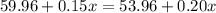
Solving for x,

`\begin{gathered} 59.96+0.15x=53.96+0.20x \\ \rightarrow59.96-53.96=0.20x-0.15x \\ \rightarrow6=0.05x \\ \rightarrow x=(6)/(0.05) \\ \Rightarrow x=120 \end{gathered}`

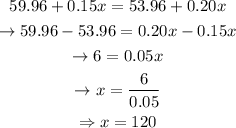
Therefore, Tom would have to drive 120 miles for the two plans to cost the same.

ANSWER: 120