For this, you can first find the annual decrease factor, like this
*You can express the percentage like this
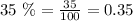
*Then, for the annual decrease factor, you have
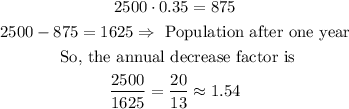
Now, the exponential decay is modeled by the equation
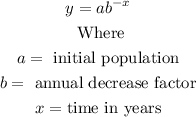
So, then the exponential function to find the population of the city after x years is
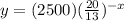
Then, the population after 5 years will be
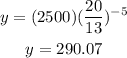
Rounding, because there are no parts of people
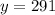
Therefore, the population after 5 years of this city will be 291 people.