Answer:
We have to use a little bit of casework to solve this problem because some numbers on the die have a positive difference of 2 when paired with either of two other numbers (for example, 3 with either 1 or 5) while other numbers will only have a positive difference of 2 when paired with one particular number (for example, 2 with 4).
If the first roll is a 1, 2, 5, or 6, there is only one second roll in each case that will satisfy the given condition, so there are 4 combinations of rolls that result in two integers with a positive difference of 2 in this case. If, however, the first roll is a 3 or a 4, in each case there will be two rolls that satisfy the given condition- 1 or 5 and 2 or 6, respectively. This gives us another 4 successful combinations for a total of 8.
Since there are 6 possible outcomes when a die is rolled, there are a total of
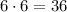 possible combinations for two rolls, which means our probability is
possible combinations for two rolls, which means our probability is
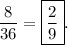
OR
We can also solve this problem by listing all the ways in which the two rolls have a positive difference of 2:
(6,4), (5,3), (4,2), (3,1), (4,6), (3,5), (2,4), (1,3).
So, we have 8 successful outcomes out of
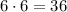 possibilities, which produces a probability of
possibilities, which produces a probability of
