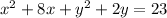For the question given, we are told to find the equation of a circle. To derive the equation we will follow the steps below.
Step 1:
Get the center of the circle
The center of the circle is the midpoint of the endpoints given
so that
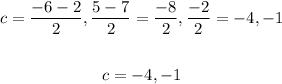
Thus the center of the circle is (-4,-1)
Step 2: Find the radius of the circle
To do this, we will get the distance between the two points and then divide it by 2
![\begin{gathered} \text{The distance betwe}en\text{ two points is given by} \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qu96w8agkwn946p6ni4dg5vmdyy9rhymmf.png)
![\begin{gathered} d=\sqrt[]{(-2+6)^2+(-7-5)^2} \\ d=\sqrt[]{4^2+(-12)^2} \\ d=\sqrt[]{16+144} \\ d=\sqrt[]{160} \\ d=4\sqrt[]{10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lap2x6tfjnfufdhkty4fgogj6tq5e7iel7.png)
Then, the radius of the circle is
![r=(d)/(2)=\frac{4\sqrt[]{10}}{2}=2\sqrt[]{10}](https://img.qammunity.org/2023/formulas/mathematics/college/psuar0tiuzt6d0xp36hk5vnyhir66cga9t.png)
Step 3: List the parameters and apply the equation of the circle

Since the center of the circle is (-4,-1) and the radius of the circle is 2√10
Then
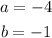
![r=2\sqrt[]{10}](https://img.qammunity.org/2023/formulas/mathematics/college/ikkmptn8xzy1ihjr3mkhmwtptclpddz1uo.png)
Step 4. Find the equation of the circle
![\begin{gathered} (x-(-4))^2+(y-(-1))^2=(2\sqrt[]{10})^2 \\ (x+4)^2+(y+1)^2=(4*10) \\ x^2+8x+16+y^2+2y+1=40 \\ x^2+8x+y^2+2y+17=40 \\ x^2+8x+y^2+2y=40-17 \\ x^2+8x+y^2+2y=23 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2a0giffmk7q2gwtndakd9344amuqe5spre.png)
Then the equation of the circle is: