In this problem, we have to compute some percentiles for a data sample. The data sample is:
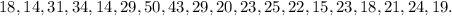
n = number of values = 19.
1) First, we order the data in ascending order:
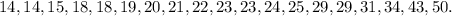
2) We calculate the rank r for the percentile p that we want to find.
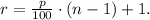
• If r is an integer then the data value at location r, x_r, is the percentile p: p = x_r.
,
• If r is not an integer, p is interpolated using ,ri,, the integer part of r, and, rf,, the fractional part of r:
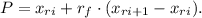
(a) for the 40th percentile, p = 40,
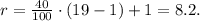
We have r = 8.2, which is not an integer, so we interpolate p using:
• ri = 8,
,
• rf = 0.2,
,
• x_ri = x_8 = 21,
,
• x_(ri + 1) = x_9 = 22.
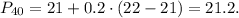
So the 40th percentile is P = 21.2.
(b) for the 75th percentile, p = 75,
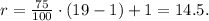
We have r = 14.5, which is not an integer, so we interpolate p using:
• ri = 14
,
• rf = 0.5
,
• x_ri = x_14 = 29
,
• x_(ri + 1) = x_15 = 29

Answers
(a) The 40th percentile: 21 (rounded to the nearest integer)
(b) The 75th percentile: 29