You have the following expression:
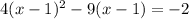
If t = x - 1, then, the previous expression can be written as follow:
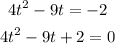
That is, you obtain a quadratic equation for t, Use the quadratic formula to find the values of t, as follow:
![\begin{gathered} t=\frac{-(-9)\pm\sqrt[]{(-9)^2-4(4)(2)}}{2(4)} \\ t=\frac{9\pm\sqrt[]{49}}{8} \\ t_1=(9+7)/(8)=(16)/(8)=2 \\ t_2=(9-7)/(8)=(2)/(8)=(1)/(4)=0.25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5p999nlgsmpabgogv760hbjhrh6g6ztefq.png)
Hence, the solutions for t are:
t = 2
t = 0.25
Now, use the previous result for t into the expression t = x - 1, to find the values of x, as follow:
t = x - 1
x = t + 1
x = 2 + 1 = 3
x = 0.25 + 1 = 1.25
Hence, the solution to the initiale quation are:
x = 1.25
x = 3