Question

calculate the wavelength in nanometers of the photon emitted when an electron transitions from the n=4 state to the n = 2 State in a hydrogen atom

Answer 1

Using the formula for change in energy,

`\Delta E=2.18*10^(-18)((1)/(n^2_1)-(1)/(n^2_2))`

where n1 and n2 are 4 and 2 respectively.

Let's calculate the change in energy when this electron makes this transition.

`\begin{gathered} \Delta E=2.18*10^(-18)((1)/(4^2)-(1)/(2^2)) \\ \Delta E=-4.0875*10^(19)J \end{gathered}`

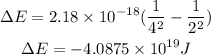
This negative value in the energy indicates that the electron jumps from a higher energy level to a lower energy level as a result of loss of energy.

From this, we can calculate the wavelength of the electron using the combination of Einstein's equation and Heisenberg's equation

`E=(hc)/(\lambda)`

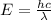
Where h = Plank's constant

c = speed of light

substitute the values into the equation and solve for the wavelength

`\begin{gathered} E=(hc)/(\lambda) \\ \lambda=(hc)/(E) \\ \lambda=(6.626*10^(-34)*3.0*10^8)/(4.0875*10^(-19)) \\ \lambda=4.86*10^(-7)m \\ \lambda=486nm \end{gathered}`

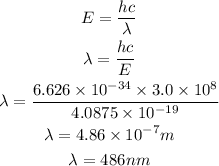
From the calculations above, the wavelength of the electron is 486nm