Question

Assuming that the rocket will splash down into the ocean, at what time down splashdown occur? How high above sea-level does the rocket get at its peak?

Answer 1

From the function of the height above sea-level given by :

`h(t)=-4.9t^2+181t+178`

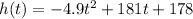
We can say that, the motion of the rocket is in parabolic since the degree of the function is 2.

Solve for the time, when the height above sea-level is 0.

Let h(t) = 0, then solve for t :

`0=-4.9t^2+181t+178`

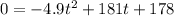
Using quadratic formula :

`t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where :

a = -4.9

b = 181

c = 178

`t=\frac{-181\pm\sqrt[]{181^2-4(-4.9)(178)}}{2(-4.9)}`
`t=\frac{-181\pm\sqrt[]{36249.8}}{-9.8}`

t = -0.96 secs and 37.90 secs

Disregard the negative value of t since there is no negative value of time

Therefore, the rocket splashes down after 37.90 seconds.

To solve for the peak of the rocket, we need to get the first derivative of the function, equate it to zero, then solve for the value of t :

Step 1 : Find the First derivative

Note that :

The derivative of

`f(x)=x^n`

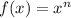
is

`f^(\prime)(x)=n* x^(n-1)`

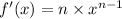
and the derivative of a constant is always 0.

`h(t)=-4.9t^2+181t+178`
`h^(\prime)(t)=2(-4.9)t+181+0`
`h^(\prime)(t)=-9.8t+181`

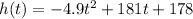
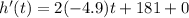
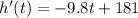
Step 2 : Equate it to 0

`0=-9.8t+181`

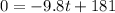
Step 3 : Solve for the value of t

`\begin{gathered} 9.8t=181 \\ t=18.469 \end{gathered}`

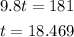
This value of t will be the time when the rocket is at it's peak.

Substitute this value of t to the function of height, will give us :

`\begin{gathered} h(t)=-4.9(18.469)^2+181(18.469)+178 \\ h(t)=1849.48 \end{gathered}`

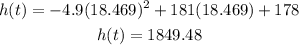
Therefore, the rocket peaks at 1849.48 meters above sea-level