To solve this question, follow the steps below.
Step 01: Substitute V0 by 112 feet per second.
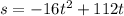
Step 02: Find t when s = 96.
To do it, first, substitute s by 96:
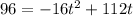
Now, subtract 96 from both sides of the equation:
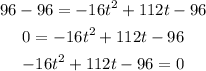
Use the Quadratic formula to find t.
For a equation ax² + bx + c = 0, x is:

In this question,
a = -16
b = 112
c = -96
Substituting in the equation to find t:
![\begin{gathered} t=(-112\pm√(112^2-4*(-16)*(-96)))/(2*(-16)) \\ t=(-112\pm√(12544-6144))/(-32) \\ t=\frac{-112\operatorname{\pm}√(6400)}{-32} \\ t=(-112\pm80)/(-32) \\ t_1=(-112-80)/(-32)=(-192)/(-32)=6 \\ t_2=(-112+80)/(-32)=(-32)/(-32)=1 \end{gathered}]()
Time to reach 96 feet = 1 or 6 seconds.
Step 03: Find the time when the projectile will return to the ground.
When the projectile return to the ground, s = 0.
Then, substitute s by 0 and find x using the same equation from step 02.

Then,
a = -16
b = 112
c = 0
Substituting in the quadratic formula:
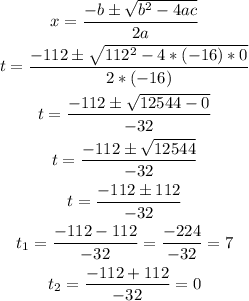
The projectile will reach the ground when t = 0 and when t = 7. t = 0 is the time when the projectile is launched and t = 7 is when the projectile returns to the ground.
(b) So, the projectile returns to the ground when t = 7 seconds.
Answer:
(a) The projectile reached 96 feet when t = 1 or t = 6 seconds.
(b) The projectile returns to the ground when t = 7 seconds.