Question

The telephone company offers two billing plans for local calls. Plan 1 charges $28 per month for unlimited calls and Plan 2 charges $13 per month plus $0.04 per call?a. Use an inequality to find the number of monthly calls for which Plan 1 is more economical than Plan 2. b. Explain the meaning of the answer to part a.

Answer 1

`a)28\leq13+0.04x\text{ Inequality(1)}`

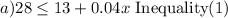
if you make more than 375 calls , is more economical the plan 1

Step-by-step explanation

Step 1

Let

Plan 1

Plan 1 charges $28 per month for unlimited calls and

`\text{Plan}1=28`

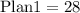
Plan 2

Plan 2 charges $13 per month plus $0.04 per call

if x representes the number of calls,then

`\begin{gathered} \text{Plan}_2=13+0.04per\text{ call} \\ \text{Plan}_2=13+0.04(x) \\ \text{Plan}_2=13+0.04x \end{gathered}`

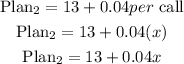
Step 2

a)Use an inequality to find the number of monthly calls for which Plan 1 is more economical than Plan 2

more economical means smaller

replacing

[tex]\begin{gathered} \text{plan}_1Step 3

solve the inequality

[tex]\begin{gathered} 28<13+0.04x \\ \text{subtract 13 in both sides} \\ 28-13<13+0.04x-13 \\ 15<0.04x \\ \text{divide both sides by 0.04} \\ \frac{15}{0.04}<\frac{0.04x}{0.04} \\ 375b)it means that if you make more than 375 , is more economical the plan 1

I hope this helps you