Solve by completing the square: x² + 12x - 6 = 0

Question

asked Sep 19, 2023 159k views

1 Answer

Adrian Florescu · Answer 1 · 2023-09-23T13:54:51+0000

Answer:

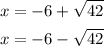
$\begin{gathered} x=-6+√(42) \\ x=-6-√(42) \end{gathered}$

Explanation:

Given the equation:

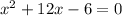
To solve the equation by completing the square, follow the steps below:

Step 1: Take the constant to the right-hand side.

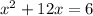
Step 2: Divide the coefficient of x by 2, square it and add it to both sides.

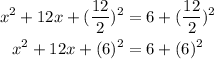
$\begin{gathered} x^2+12x+((12)/(2))^2=6+((12)/(2))^2 \\ x^2+12x+(6)^2=6+(6)^2 \end{gathered}$

Step 3: Write the left-hand side as a perfect square.

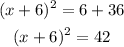
$\begin{gathered} (x+6)^2=6+36 \\ (x+6)^2=42 \end{gathered}$

Step 4: Take the square root of both sides.

$\begin{gathered} √((x+6)^2)=\pm√(42) \\ x+6=\pm√(42) \end{gathered}$

Step 5: Solve for x.

$\begin{gathered} x=-6\operatorname{\pm}√(42) \\ \implies x=-6+√(42),x=-6-√(42) \end{gathered}$