Question

Write an equation that represents the following situations. Then, solve the equations. 1) Heidi designs office furniture. Her latest project is a tabletop in the shape of a trapezoid with two rectangles cut out for a computer station. Each rectangle has an area of 12 The following is the design of the table. 287 h - 8 in In 10 in 10 in 163 in If Heidi needs to cover the desktop with a glass panel that also has the cutouts, what is the area of the glass panel?a. Write the equation in words. b. Calculate the two areas. A. = A = c. Choose a variable for the unknown quantity and write the equation with the substituted values. d. Solve the equation. Include appropriate units in your answer.

Answer 1

a) Area of that trapezoid - the areas of those 2 rectangles.

b) 153 1/4 in²

a) Let's start by deriving that equation from the areas of the trapezoid minus the area of those rectangles.

Area of the glass panel:

Area of that trapezoid - the areas of those 2 rectangles.

b) Before calculating those two areas, let's convert those mixed numbers into improper fractions to make our calculations easier:

`\begin{gathered} 12(3)/(8)=(12*8+3)/(8)=(96+3)/(8)=(99)/(8) \\ 28(1)/(4)=(28*4+1)/(4)=(113)/(4) \\ 16(1)/(4)=(64+1)/(4)=(65)/(4) \end{gathered}`

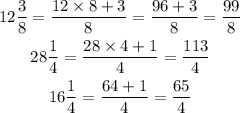
Note that we've kept the original denominator and rewrote the numerator as the product of the bottom number by the whole one adding to the numerator.

Area of the Trapezoid:

`A=((B+b)h)/(2)\Rightarrow A=(((113)/(4)+(65)/(4))\cdot8)/(2)=178in^2`

Area of those two rectangles:

`\begin{gathered} A_2=(99)/(8)*2 \\ A_2=(99)/(4) \end{gathered}`

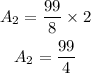
Area of the glass panel:

`\begin{gathered} A\text{ =}178-(99)/(4) \\ A=(613)/(4)\text{ or A=153}(1)/(4) \end{gathered}`

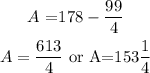
3) Hence, the answers are:

a) Area of that trapezoid - the areas of those 2 rectangles.

b) 153 1/4 in² (Mixed Number)