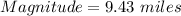Step-by-step explanation:
Given;
We are given the directions taken by a mouse trapped in a maze.
To find its way out, it takes;
(a) 15 miles east
(b) Makes a 90 degree left turn
(c) Walks 8 miles
(d) Makes another 90 degree left turn
(e) Walks another 10 miles
Required;
We are required to find the magnitude of the resultant vector.
Step-by-step solution;
To do this, let us represent the movements from (a) to (e) on a diagram. This is shown below;
From the diagram above, we can see that the magnitude is the distance from the endpoint to the starting point and that has resulted in a side length that can be solved using the Pythagoras' theorem, as shown below;
Pythagoras' Theorem:
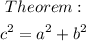
Where the variables are;

We can now substitute the values given and solve as follows;

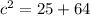

Take the square root of both sides;
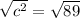
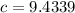
Rounded to 2 decimal places, the magnitude of the resultant vector is;
ANSWER: