On the plane
Therefore, AB and DC are parallel sides, and so are BC and AD.
We need to calculate the length of 2 perpendicular sides, for example, AB and BC.
In general, the formula to get the distance between two points is
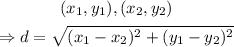
Thus, in our case,
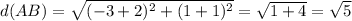
and
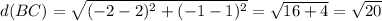
Therefore, the area is
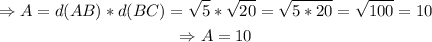
Thus, the area is 10, option B.