Question

Which of the following answers is equivalent to x4 + 4X3 + 6x2 + 4x +1 (4x + 1) raised to the power of 4 (x + 1) raised to the power of 4. (2x + 1) raised to the power of 4 (2x - 1) raised to the power of 4

Answer 1

b. (x + 1) raised to the power of 4.

Step-by-step explanation:

To know the answer, we need to solve the expression of every answer and compare the result with the initial expression.

So, (4x +1) raised to the power of 4 is equal to:

`(4x+1)^4=(4x+1)(4x+1)(4x+1)(4x+1)`

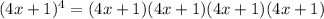
Applying the distributive property, we get:

`\begin{gathered} (4x+1)^4=(16x^2+8x+1)(4x+1)(4x+1) \\ (4x+1)^4=(64x^3+48x^2+12x+1)(4x+1) \\ (4x+1)^4=256x^4+256x^3+96x^2+16x+1 \end{gathered}`

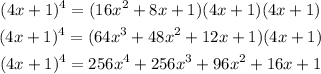
Therefore, this is not the correct answer:

In the same way, (x + 1) raised to the power of 4 is equal to:

`\begin{gathered} (x+1)^4=(x+1)(x+1)(x+1)(x+1) \\ (x+1)^4=(x^2+2x+1)(x+1)(x+1) \\ (x+1)^4=(x^3+3x^2+3x+1)(x+1) \\ (x+1)^4=x^4+4x^3+6x^2+4x+1 \end{gathered}`

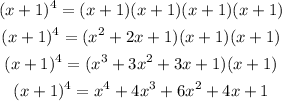
Since this is equal to the initial expression, the correct answer is b. (x + 1) raised to the power of 4.