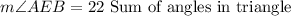We know that the interior angles of any triangle have to add 180°, we know angles AEC and angles EAC from triangle AEC, then we have that the next step is:

Now, since line BE and EC are congruent this means that triangle BCE is isosceles, and then the next step would be:
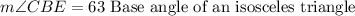
We notice that angles CBE and ABE form a linear pair, then we have:
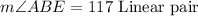
Finally, once again we use the fact that the sum of interior angles is equal to 180°, then we have: