Question

The six trigonometric functions are not invertible. What has to be done to make them invertible?

Answer 1

Step 1

The six trigonometric functions are;

`Sine,\text{ cosine, tangent, cotangent, secant, cosecant.}`

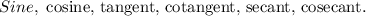
In general, a function is invertible only if each input has a unique output. That is, each output is paired with exactly one input. That way, when the mapping is reversed, it will still be a function!

Step 2

These trigonometric functions are not invertible. To make them invertible we must restrict their domains to form a new function in which there is at most one x-value for each y-value

Answer; To make them invertible we must restrict their domains to form a new function in which there is at most one x-value for each y-value