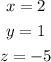Question

What is the solution to the system(1)2x-y+z=-2(2)x+3y-z=10(3)x+2z=-8

Answer 1

Let's clear y in (1) and plug in (2):

`\begin{gathered} 2x-y+z=-2 \\ \rightarrow2x+z+2=y \\ \\ x+3y-z=10 \\ \rightarrow x+3(2x+z+2)-z=10 \\ \rightarrow x+6x+3z+6-z=10 \\ \rightarrow7x+2z=4 \end{gathered}`

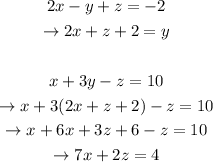
With this new equation and with (3), we'll have the following system:

`\begin{cases}7x+2z=4 \\ x+2z=-8\end{cases}`

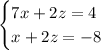
Let's multiply (3) by -1 and add up both equations. Then, we can solve for x :

`\begin{gathered} \begin{cases}7x+2z=4 \\ x+2z=-8\end{cases}\rightarrow\begin{cases}7x+2z=4 \\ -x-2z=8\end{cases} \\ \\ \rightarrow6x=12\rightarrow x=(12)/(6) \\ \\ \Rightarrow x=2 \end{gathered}`

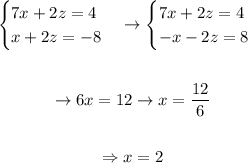
Let's plug in this value in (3) and solve for z :

`\begin{gathered} x+2z=-8 \\ \rightarrow2+2z=-8 \\ \rightarrow2z=-10\rightarrow z=-(10)/(2) \\ \Rightarrow z=-5 \end{gathered}`

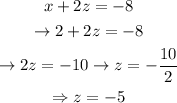
Since we already have an expression for y in terms of x and z, we can find y :

`\begin{gathered} 2x+z+2=y \\ \rightarrow y=2(2)-5+2 \\ \\ \Rightarrow y=1 \end{gathered}`

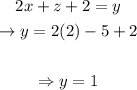
Therefore, the solution to our system would be:

`\begin{gathered} x=2 \\ y=1 \\ z=-5 \end{gathered}`