Question

Two resistors of 5.0 ohm and 9.0 ohm are connected in parallel. A 4.0-ohm resistor is then connected in series with the parallel combination. A 6.0-V battery is then connected to the series-parallel combination. What is the current through the 4.0-ohm resistor? zero 0.53 A 0.83 A 0.30 A

Answer 1

Given:

The resistances are

`\begin{gathered} R_1=5.0\text{ }\Omega \\ R_2=9.0\text{ }\Omega \\ R_3=4.0\text{ }\Omega \end{gathered}`

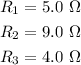
The potential of the battery is

`V=6.0\text{ V}`

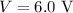
To find:

The current through the 4.0-ohm resistor

Step-by-step explanation:

The equivalent resistance of the circuit is,

`\begin{gathered} R_(eq)=R_1\parallel R_2+R_3 \\ =5.0\parallel9.0+4.0 \\ =(5.0*9.0)/(5.0+9.0)+4.0 \\ =3.2+4.0 \\ =7.2\text{ }\Omega \end{gathered}`

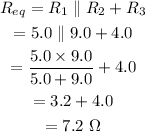
The current in the circuit is,

`\begin{gathered} i=(V)/(R_(eq)) \\ =(6.0)/(7.2) \\ =0.83\text{ A} \end{gathered}`

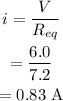
For the series combination, the same current flows through the 4.0-ohm resistance and the parallel combination of 5.0 and 9.0-ohm resistances.

Hence, the current through 4.0 ohm is 0.83 A.