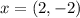The given equation is
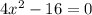
We will factor the given equation using the difference of squares formula given below
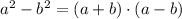
So, we have
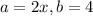
Applying the above formula will result in,
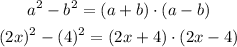
Therefore, the factors of the given equation are
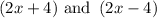
Bonus:
You can find the possible values of x by equating the factors to zero.
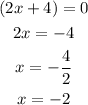
Similarly,
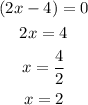
So, the possible values of x are