Start by calling the first number as a variable:

then, since this number exceeds the other number by 5, the other number is:
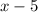
then, write the equation that represents the sum of their square,
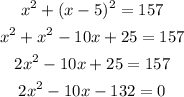
solve using the quadratic:
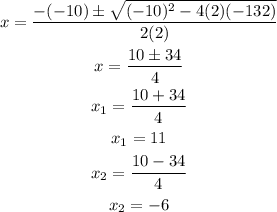
Answer:
since the result gives two answers there are two possible combinations that fulfill this statement;
in the first case 11 and 6, for the second case -11 and -6.