Question

What are the coordinates of point Q? Explain your answer. Using the information in the figure, show thatthe length of the median MQ is half the length of the hypotenuse of A MRP. Provide an argumentsupported by valid mathematical reasoning and/or calculations.

Answer 1

The median of a triangle is a line segment that joins one of the vertices with the midpoint of the opposite line.

If line segment MQ is the median of the triangle, the point Q is the midpoint of the opposite side RP.

To calculate the coordinates of Q, you have to use the coordinates of the endpoints of side RP.

R(0,2b)

P(2a,0)

x-coordinate of Q

Calculate the difference between the x-coordinates of points R and P:

`x_P-x_R=2a-0=2a`

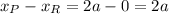
Divide the distance between both coordinates by 2 to determine the distance over the x-axis between the endpoints and the midpoint

`(2a)/(2)=a`

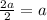
Add this distance to the x-coordinate of R to determine the x-coordinate of Q

`\begin{gathered} x_Q=0+a \\ x_Q=a \end{gathered}`

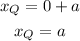
y-coordinate of Q

Calculate the difference between the y-coordinates of points R and P

`y_P-y_R=0-2b=-2b`

Divide the result by 2

`-(2b)/(2)=-b`

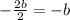
Add it to the y-coordinate of point R to determine the y-coordinate of Q

`\begin{gathered} y_Q=2b+\left(-b\right) \\ y_Q=b \end{gathered}`

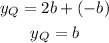
The coordinates of Q are (a,b)

To determine that the length of the median MQ is half the length of the hypothenuse RP, you have to apply the following formula to calculate the distance between two points:

`d=√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

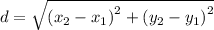
Length MQ

Consider M(0,0) as (x₁,y₁) and Q(a,b) as (x₂,y₂)

`\begin{gathered} MQ=√(\lparen a-0^)^2+\left(b-0\right)^2) \\ MQ=√(a^2+b^2) \end{gathered}`

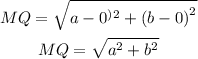
The half of the hypothenuse RP is represented by the segments RQ and QP, using the formula of the distance between two points, you can calculate the length on either one of the line segments, for example, the length of RQ.

Consider R(0,2b) as (x₁,y₁) and Q(a,b) as (x₂,y₂)

`\begin{gathered} RQ=√(\left(a-0\right)^2+\left(b-2b\right)^2) \\ RQ=√(a^2+\left(-b\right)^2) \\ RQ=√(a^2+b^2) \end{gathered}`

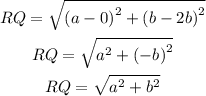
As you can see the median MQ is equal to half the hypothenuse.