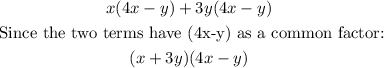Question

Factor this polynomial. The image is attached here. Need help!

Answer 1

`4x^2+11xy-3y^2=(x+3y)(4x-y)`

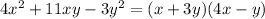
Explanation:

To factor the following polynomial, break the expression into groups:

The grouping method can be used to factor polynomials whenever a common factor exists between the groupings. Just find families easier-to-factor groups that we can better approach the problem.

`\begin{gathered} 4x^2+11xy-3y^2 \\ (4x^2-xy)+(12xy-3y^2) \end{gathered}`

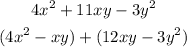
Then, factor it using factor by grouping:

`\begin{gathered} x(4x-y)+3y(4x-y) \\ \text{ Since the two terms have (4x-y) as a common factor:} \\ (x+3y)(4x-y) \end{gathered}`