Question

Fine the end behavior and x-value of holeEquation is to the right

Answer 1

Given the function:

`\: f\mleft(x\mright)=(x+1)/(\left(x-3\right)\left(x^2-1\right))`

The end behaviour of the function f(x) describes the behaviour of the function as x approaches +∞ and -∞.

When x approaches +∞,

`\lim _(x\rightarrow\infty)f(x)=\text{ }\lim _(x\rightarrow\infty)(x+1)/((x-3)(x^2-1))=0`

Thus, as x approaches +∞, the function f(x) approaches zero.

When x approaches -∞,

`\lim _(x\rightarrow-\infty)f(x)=\text{ }\lim _(x\rightarrow-\infty)(x+1)/((x-3)(x^2-1))=0`

Thus, as x approaches -∞, the function f(x) approaches zero.

x-value of the hole:

For a rational function f(x) given as

`f(x)=(p(x))/(q(x))`

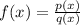
Provided that p(x) and q(x) have a common factor (x-a), the function f(x) will have a hole at x=a.

Thus, from the function f(x)

`f(x)=(x+1)/((x-3)(x^2-1))`

by expansion, we have

`f(x)=\frac{x+1}{(x-3)(x^{}-1)(x+1)}`

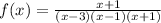
The expression (x-1) is a common factor of the numerator and the denominator.

Thus,

`\begin{gathered} x-1=0 \\ \Rightarrow x=1 \end{gathered}`

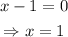
Hence, the x-value of the hole is 1.