Question

Create your own quadratic equation whilst explaining how to use the quadratic formula to solve it. Be specific, using a, b, and c of your equation and give solutions to theequation you chose.

Answer 1

Let the quadratic equation is

`x^2-8x+16=0`

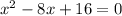
Here, a is the coefficient of x^2, b is the coefficient of x and c is the constant.

For the equation we have a = 1, b = -8 and c = 16.

We know that the quadratic formula is given by:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

So, the solution of the quadratic equation is:

`\begin{gathered} x=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(1)(16)}}{2(1)} \\ x=\frac{8\pm\sqrt[]{64-64}}{2} \\ x=\frac{8\pm\sqrt[]{0}}{2} \\ x=(8)/(2) \\ x=4 \end{gathered}`

Thus, there are two real and equal solutions for the given quadratic equation that is x = 4 and x = 4.