We have the function f(t) defined as:
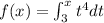
We have to find f'(x).
We can solve this integral as:
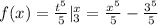
If we derive this expression for f(x) we obtain:
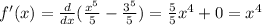
NOTE: This expression could have been derived from the function inside the integral.
We can now find f'(3) as:
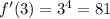
Answer:
f'(x) = x^4
f'(3) = 81