Step-by-step explanation:
The total number of students in the algebra class is given below as
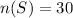
The number of girsl who won a graphing calculator is given below as
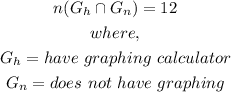
Concept:
To figure out the probabaility that a randomly chosen student will be a girl and own a graphing calculator, we will use the formula below
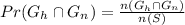
By substituting the values, we will have
![\begin{gathered} Pr(G_(h)\operatorname{\cap}G_(n))=\frac{n(G_(h)\operatorname{\cap}G_(n))}{n(S)} \\ Pr(G_h\operatorname{\cap}G_n)=(12)/(30) \\ Pr(G_h\operatorname{\cap}G_n)=(2)/(5) \end{gathered}]()
Hence,
The final answer is
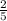
The FOUTH OPTION is the correct answer