Let's draw the figure to better understand the scenario:
Let,
s = the measure of the sides of the square
For us to be able to determine the area, let's first find out the measure of its side.
We will be using the Pythagorean Theorem:

![\text{ s}^2+\text{ s}^2=(4\sqrt[]{2})^2](https://img.qammunity.org/2023/formulas/mathematics/college/tkvnsrudlic3kzavuvga8p1x8aurz02nc4.png)

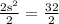

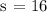
Let's now determine the area of the square:
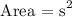
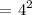

Therefore, the area of the square is 16.