Given:
The change in volume by time is, (dV/dt) = 10 cubic feet per minute.
The diameter and height of the right circular one are equal, 2r = h.
Height of the pile is, h = 21 ft.
The objective is to find the rate of increase in height of the pile.
Step-by-step explanation:
The general formula of volume of cone is,
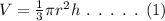
From the given data, radius of the cone can be calculated as,

Substitute the value of r in equation (1).
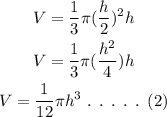
To find rate of increase in height of the pile:
Now, differentiate equation (2) with respect to time t.
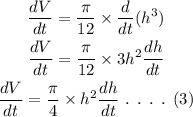
Substitute (dV/dt) and h in equation (3).
On plugging the obtained values in eqation (3),
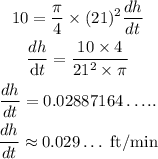
Hence, the rate of increase in height of the pile is 0.029 ft/min.