Question

Polygon BCDE ≅ polygon RSTU. Find the value of X and the value of Y

Answer 1

By comparing both polygons, we can tell that they are not the same polygon, since one of the sides has length 11 in one trapezoid and 12 in the other. So, this polygons are similar. We notice that the variables X and Y are part of the angles. In polygons that are similar, the measure of the homologous angles are equal. By homologous we mean angles that are located at the same place in both figures. To determine the homologous angles, we should have both figures drawn in the same orientation. To do so, we will flip the trapezoid on the left, so its orientation matches the one fromt the right. I picture of this flipping would be

From this picture, by comparing it to the other polygon, we determine that the angle EDC is homologous to the angle UTS. So, their measure should be the same. So, we get the following equation

`2y\text{ - 37 = }y+2`

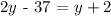
By adding 37 on both sides and subtracting y on both sides, we get

`2y\text{-y = +2 +37 = 39}`

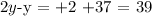
This implies that y = 39°.

By doing the same procedure, we find that the angles URS and CBE are homologous. So their measures are equal and we get the equation

`51\text{ = }2x+13`

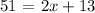
Then, by subtracting 13 on both sides

`2x\text{ = 51-13 = 38}`

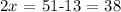
If we divide both sides by 2 we get

`x=(38)/(2)=19`

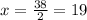
So x = 19°.