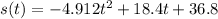
1) To find when the object strikes the ground, we need to find the roots of the equation. Using quadratic formula:
![\begin{gathered} t_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t_(1,2)=\frac{-18.4\pm\sqrt[]{18.4^2-4(-4.912)(36.8)}}{2(-4.912)} \\ t_(1,2)=\frac{-18.4\pm\sqrt[]{1061.6064}}{-9.824} \\ \\ t_1=(-18.4+32.582)/(-9.824)=-1.44 \\ t_2=(-18.4-32.582)/(-9.824)=5.2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nh2xn9rwgeqia4o19vbtjufmojt9ct6si0.png)
t can't be negative, then the object strikes the ground after 5.2 seconds
2) The maximum height is the vertex of the parabola. The t-coordinate is computed as follows:
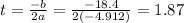
It takes 1.87 seconds for the object to get to its maximum height
3) To find the height after 3.32 seconds, we have to replace t = 3.32 int the equation:
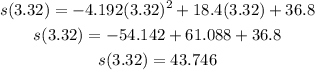
The height was 43.746 meters