We are asked to determine the probability of rolling a 6 and then rolling a number less than 2. To do that we will use the product rule probabilities since we want to find the probability of two independent events happening:
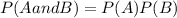
Where:
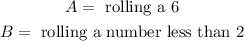
To determine the probability of rolling a 6 we need to have into account that there are 6 possible outcomes out of which only one is a 6. Therefore, the probability is:
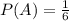
To determine the probability of B we need to have into account that in a 6-sided die the numbers that are less than 2 are (1), this means that there is only one number less than 2 out of 6 possible numbers. Therefore, the probability is:

Now, we substitute in the product rule:
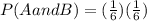
Solving the product:
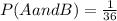
Therefore, the probability is 1/36.