Question

Joan invests $200. She earns interest at 3% per annum, compounded monthly.What is the future value of Joan’s investment after 1.5 years?

Answer 1

For this exercise you need to use the following formula:

`FV=PV\mleft(1+r\mright)^n`

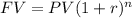
Where "FV" is the future value, "PV" is the present value, "r" is the interest rate (in decimal form), and "n" number of periods.

In this case, analyzing the information given in the exercise, you can identify that:

`PV=200`

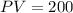
Remember that a percent can be written in Decimal form by dividing it by 100. Then:

`(3)/(100)=0.03`

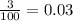
Since she earns interest at 3% per annum and it is compounded monthly, you can determine that the interest rate per month is:

`r=(0.03)/(12)=0.0025`

Knowing that 1 year has 12 months, you know that:

`(12)(1.5\text{ }years)=18\text{ }months`

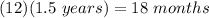
Then:

`n=18`

Therefore, you can substitute all those values into the formula and then evaluate, in order to find the future value of Joan’s investment after 1.5 years:

`\begin{gathered} FV=PV(1+r)^n \\ FV=(200)(1+0.0025)^(18) \\ FV=(200)(1.0025)^(18) \end{gathered}`
`FV\approx209.19`

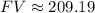
Hence, the answer is: $209.19 (approximately).