Question

Determine the open intervals on which the function is increasing, decreasing, or constant.(Enter your answers using interval notation. If an answer does not exist, enter DNE.)

Answer 1

Given:

`f(x)=√(x^2-4)`

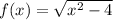
To find:

The interval at which the function is increasing, decreasing and constant.

Step-by-step explanation:

We know that,

For a function, y = F(x), if the value of y is increasing on increasing the value of x, then the function is known as an increasing function.

For a function, y = F(x), if the value of y is decreasing on increasing the value of x, then the function is known as a decreasing function.

According to the graph,

The function is increasing in the interval,

`[2,\infty)`

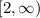
Because, if x increases from 2, the value of y increases.

The function is decreasing in the interval,

`(-\infty,-2]`

Because, if x increases from negative infinity, the value of y decreases.

As we know, a constant function is a function whose output value is the same for every input value.

Here, the function is not constant at any of the intervals.

Final answer:

Increasing:

`[2,\infty)`

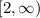
Decreasing:

`(-\infty,-2]`

Constant: DNE.